Specifications PyCSP³ Tools Instances Competitions About

Constraint MDD

The constraint mdd, see [CY08], [CY10] and [PR14], ensures that the sequence of values assigned to the variables it involves follows a path going from the root of the described MDD (Multi-valued Decision Diagram) to the unique terminal node.

mdd($X$,$M$) with $X=\langle x_1,x_2,\ldots,x_r \rangle$ and $M$ a MDD, iff $x_1 x_2 \ldots x_r \in L(M)$ where $L(M)$ denotes the language recognized by the MDD $M$.

Because the graph is directed, acyclic, with only one root node and only one terminal node, we just need to introduce transitions. The syntax for mdd is:

Syntax

 <mdd>
  <list> (intVar wspace)+ </list>
  <transitions> ("(" state "," intVal "," state ")")+ </transitions>
</mdd>

As an example, the constraint of scope $\langle x_1,x_2,x_3 \rangle$ is defined from the simple MDD depicted below (with root node r and terminal node t) as:

mdd

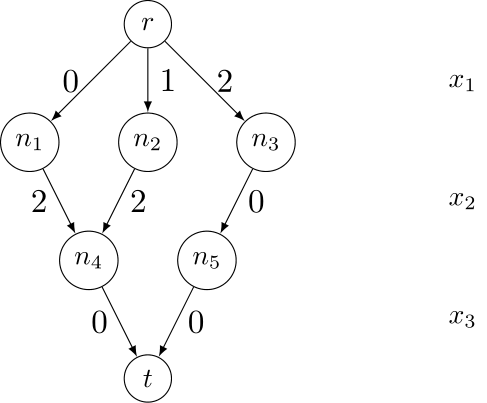
We obtain:

Example

<mdd>
  <list> x1 x2 x3 </list>
  <transitions>
    (r,0,n1)(r,1,n2)(r,2,n3)
    (n1,2,n4)(n2,2,n4)(n3,0,n5)
    (n4,0,t)(n5,0,t) 
  </transitions>
</mdd>