Skeleton
To begin with, below, you will find the syntactic form of the skeleton of a typical XCSP3 problem instance, i.e., the skeleton used by most (Syntactic details for various frameworks are given in the full specifications} of the frameworks recognized by XCSP3. In our syntax, we combine XML and BNF. XML is used for describing the main elements and attributes of XCSP3, whereas BNF is typically used for describing the textual contents of XCSP3 elements and attributes, with in particular |, [ ], ( ), * and + respectively standing for alternation, optional character, grouping and repetitions (0 or more, and 1 or more). Note that {tag(“elt…”)} denotes an XML element of name elt whose description is given later in the specifications (this is the meaning of …). Some strings refer to BNF non-terminals. For example, frameworkType corresponds to a token chosen among CSP, COP, WCSP, … Also, for the sake of simplicity, we write constraint and metaConstraint for respectively denoting any constraint element such as e.g., extension or allDifferent, and any meta-constraint such as e.g., slide or not.
Syntax
<instance format="XCSP<sup>3</sup>" type="frameworkType">
<variables>
( <var .../>
| <array .../>
)+
</variables>
<constraints>
( <constraint .../>
| <metaConstraint .../>
| <group .../>
| <block .../>
)*
</constraints>
[<objectives [ combination="combinationType" ]>
( <minimize .../>
| <maximize .../>
)+
</objectives>]
[<annotations .../>]
</instance>
As you can observe, a typical instance is composed of variables, constraints, and possibly objectives (and annotations). Variables are declared stand-alone (element var or under the form of arrays (element array. Constraints can be elementary or more complex (meta-constraints). Constraints can also be posted in groups and/or declared in blocks; group and block correspond to structural mechanisms. Finally, any objective boils down to minimizing or maximizing a certain function, and is represented by an element minimize or maximize.
For a first illustration of XCSP3, let us consider the small constraint network depicted (by its compatibility graph) in the following figure.
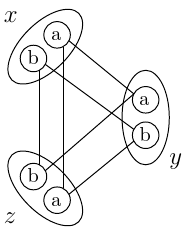
We have here three symbolic variables, x, y, z of domain {a,b} and three binary constraints, one per pair of variables. An edge in this graph means a compatibility between two values of two different variables. In XCSP3, we obtain:
Example
<instance format="XCSP<sup>3</sup>" type="CSP">
<variables>
<var id="x"> a b </var>
<var id="y"> a b </var>
<var id="z"> a b </var>
</variables>
<constraints>
<extension>
<list> x y </list>
<supports> (a,a)(b,b) </supports>
</extension>
<extension>
<list> x z </list>
<supports> (a,a)(b,b) </supports>
</extension>
<extension>
<list> y z </list>
<supports> (a,b)(b,a) </supports>
</extension>
</constraints>
</instance>
Of course, we shall give all details of this representation in the next sections, but certainly you are comfortable to make the correspondence between the figure and the XCSP3 code. If you pay attention to the constraints, you can detect that two of them are similar. Indeed, the list of supports (compatible pairs) between x and y is the same as that between x and z. In XCSP3, it is possible to avoid such redundancy by using either the concept of constraint group or the attribute as. Also, because the three variables share the same type and the same domain, it is possible to avoid redundancy by using either the concept of variable array or the attribute as. We shall describe all these concepts later.
As a second illustration, we consider the arithmetic optimization example introduced in the Minizinc Tutorial:
``A banana cake which takes 250g of self-raising flour, 2 mashed bananas, 75g sugar and 100g of butter, and a chocolate cake which takes 200g of self-raising flour, 75g of cocoa, 150g sugar and 150g of butter. We can sell a chocolate cake for $\$4.50$ and a banana cake for $\$4.00$. And we have 4kg self-raising flour, 6 bananas, 2kg of sugar, 500g of butter and 500g of cocoa. The question is how many of each sort of cake should we bake for the fete to maximize the profit?''
Here is how this small problem can be encoded in XCSP3. Surely, you can analyze this piece of code (if you are told that le stands for “less than or equal to”). Notice that any XCSP3 element can be given the optional attribute note, which is used as a short comment.
Example
<instance format="XCSP<sup>3</sup>" type="COP">
<variables>
<var id="b" note="number of banana cakes"> 0..100 </var>
<var id="c" note="number of chocolate cakes"> 0..100 </var>
</variables>
<constraints>
<intension> le(add(mul(250,b),mul(200,c)),4000) </intension>
<intension> le(mul(2,b),6) </intension>
<intension> le(add(mul(75,b),mul(150,c)),2000) </intension>
<intension> le(add(mul(100,b),mul(150,c)),500) </intension>
<intension> le(mul(75,c),500) </intension>
</constraints>
<objectives>
<maximize> add(mul(b,400),mul(c,450)) </maximize>
</objectives>
</instance>
As we shall see, we can group together the constraints that share the same syntax (by introducing so-called constraint templates, which are abstract forms of constraints with parameters written %i) and we can describe specialized forms of objectives. An equivalent representation of the previous instance is:
Example
<instance format="XCSP<sup>3</sup>" type="COP">
<variables>
<var id="b" note="number of banana cakes"> 0..99 </var>
<var id="c" note="number of chocolate cakes"> 0..99 </var>
</variables>
<constraints>
<group>
<intension> le(add(mul(%0,%1),mul(%2,%3)),%4) </intension>
<args> 250 b 200 c 4000 </args>
<args> 75 b 150 c 2000 </args>
<args> 100 b 150 c 500 </args>
</group>
<group>
<intension> le(mul(%0,%1),%2) </intension>
<args> 2 b 6 </args>
<args> 75 c 500 </args>
</group>
</constraints>
<objectives>
<maximize type="sum">
<list> b c </list>
<coeffs> 400 450 </coeffs>
</maximize>
</objectives>
</instance>
Alternatively, we could even use the global constraint sum, so as to obtain:
Example
<instance format="XCSP<sup>3</sup>" type="COP">
<variables>
<var id="b" note="number of banana cakes"> 0..99 </var>
<var id="c" note="number of chocolate cakes"> 0..99 </var>
</variables>
<constraints>
<sum note="using the 4000 grams of flour">
<list> b c </list>
<coeffs> 250 200 </coeffs>
<condition> (le,4000) </condition>
</sum>
<sum note="using the 6 bananas">
<list> b </list>
<coeffs> 2 </coeffs>
<condition> (le,6) </condition>
</sum>
<sum note="using the 2000 grams of sugar">
<list> b c </list>
<coeffs> 75 150 </coeffs>
<condition> (le,2000) </condition>
</sum>
<sum note="using the 500 grams of butter">
<list> b c </list>
<coeffs> 100 150 </coeffs>
<condition> (le,500) </condition>
</sum>
<sum note="using the 500 grams of cocoa">
<list> c </list>
<coeffs> 75 </coeffs>
<condition> (le,500) </condition>
</sum>
</constraints>
<objectives>
<maximize type="sum" note="receiving 400 and 450 cents for each banana and chocolate cake, respectively">
<list> b c </list>
<coeffs> 400 450 </coeffs>
</maximize>
</objectives>
</instance>